

Siguiente: Método del cociente de uniformes
Nivel anterior: Métodos generales de generación de vv.aa.
Previa: Método de aceptación y rechazo
Sea f(x) la función de densidad de una variable aleatoria X.
El método de composición consiste en lo siguiente:
- 1.
- Se descompone f como
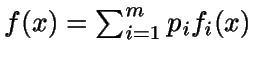 ,
con fi
función de densidad,
,
con fi
función de densidad, 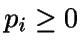 ,
,
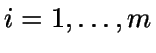 ,
,
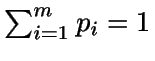 .
.
- 2.
- Se elige la i-ésima función con probabilidad pi y se genera
un valor para la función de densidad fi.
Ejemplo:
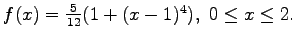
La función de distribución es
por lo que no se puede aplicar el método de la transformación
inversa. Sin embargo, si hacemos
entonces
y podemos aplicar el método de composición.
El método queda:
- 1.
- Se genera u1, u2 con distribución U(0,1).
- 2.
- Si
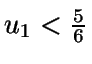 ,
entonces x=2u2. En caso contrario,
,
entonces x=2u2. En caso contrario,
![$x=1+\sqrt[5]{2u_2-1}$](img460.gif) .
.
Ejemplo:
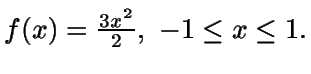
Hacemos
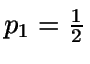 ,
,
![$f_1=3x^2 \chi_{[-1,0]}$](img463.gif) ,
,
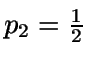 y
y
![$f_2=3x^2 \chi_{[0,1]}$](img465.gif) .
.
Método:
- 1.
- Se genera u1, u2 según U(0,1).
- 2.
- Si
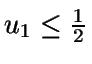 ,
entonces
,
entonces
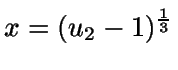 .
En
caso contrario, se hace
.
En
caso contrario, se hace
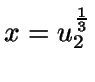 .
.
