

Siguiente: Método de composición
Nivel anterior: Métodos generales de generación de vv.aa.
Previa: Método de la transformación inversa
Sea X una variable aleatoria con función de densidad
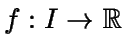 .
Supóngase que f(x)=Cg(x)h(x) con
C una constante,
.
Supóngase que f(x)=Cg(x)h(x) con
C una constante, 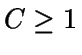 ,
,
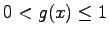 y h(x) una
función de densidad en I. Si
y h(x) una
función de densidad en I. Si
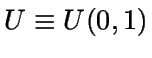 e Y (con función
de densidad h) son independientes, entonces
e Y (con función
de densidad h) son independientes, entonces
Demostración:
Q.E.D.
Algoritmo de aceptación y rechazo:
- 1.
- Se genera
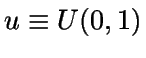 y un valor y de la variable Y (de
forma independiente).
y un valor y de la variable Y (de
forma independiente).
- 2.
- Si u>g(y), se va al paso 1.
- 3.
- Si
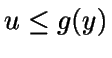 ,
entonces se hace x=y.
,
entonces se hace x=y.
Ahora interesa conocer cuál es la probabilidad de que en una
iteración concreta se rechace el valor generado:
Como el número de iteraciones del método hasta aceptar un valor
sigue una distribución geométrica de parámetro
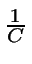 (cuya
esperanza es C), entonces si queremos optimizar el método habrá
que intentaar que C sea próxima a uno y
que h sea sencilla de generar.
(cuya
esperanza es C), entonces si queremos optimizar el método habrá
que intentaar que C sea próxima a uno y
que h sea sencilla de generar.
Si hacemos
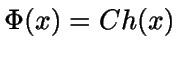 ,
entonces buscamos que sea
,
entonces buscamos que sea
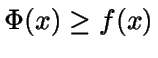 .
Se tendrá
.
Se tendrá
Como 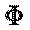 coincide con h salvo la constante y h es
una función de densidad en I, entonces también se tiene que
cumplir que
coincide con h salvo la constante y h es
una función de densidad en I, entonces también se tiene que
cumplir que
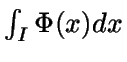 sea finita.
sea finita.
Caso particular: f acotada, definida en un intervalo [a,b] acotado
Sea 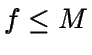 en I=[a,b].
en I=[a,b].
En este caso tomamos 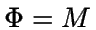 .
Así
.
Así
H-1(u)= a + (b-a)u.
Además,
El algortimo resultante es:
- 1.
- Genérese u1,
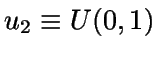 de forma independiente.
de forma independiente.
- 2.
Si
Mu1 > f(a+(b-a)u2), entonces se vuelve al paso 1.
En caso contrario, se hace
x=a+(b-a)u2.
Ejemplo:
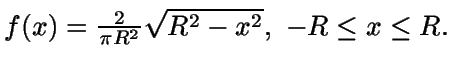
En este caso [a,b]=[-R,R], por lo que
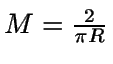 ,
pues
f alcanza su máximo en x=0. Tratemos de simplificar el test
de aceptación
,
pues
f alcanza su máximo en x=0. Tratemos de simplificar el test
de aceptación
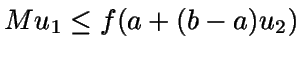 .
.
si y sólo si
si y sólo si
si y sólo si
La probabilidad de aceptación es
Ejemplo:
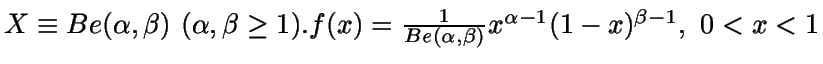 .
La función
.
La función
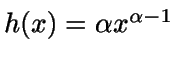 es función de densidad en
(0,1). Así
es función de densidad en
(0,1). Así
Tomamos
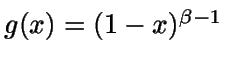 .
De este modo se tiene que
.
De este modo se tiene que
y el criterio de aceptación es
tomándose
Ejemplo:
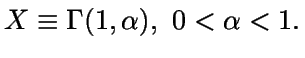
Para que se cumplan todas las condiciones que necesitamos, tomamos
Es inmediato que
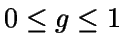 .
Veamos que
.
Veamos que 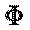 integra un valor finito:
integra un valor finito:
Ahora
Como
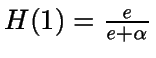 ,
entonces
,
entonces
El algoritmo para simular la variable X es:
- 1.
- Se genera u1, u2 según una distribución U(0,1).
- 2.
- Si
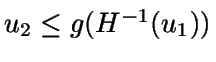 ,
entonces se toma
x=H-1(u1). En
caso contrario, se repite el paso 1.
,
entonces se toma
x=H-1(u1). En
caso contrario, se repite el paso 1.

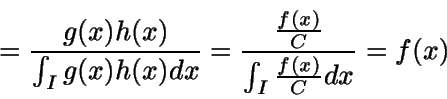
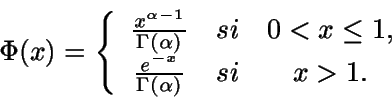
![\begin{displaymath}C=\int_0^{+\infty} {\Phi(x)} dx = \frac
{1}{\Gamma(\alpha)} ...
...ha} \right]_0^1 + \left [
-e^{-x} \right]_1^{+\infty} \right)=\end{displaymath}](img439.gif)