Siguiente: Modelo 6 Nivel anterior: Modelos de inventario con revisión continua Previa: Modelo 4

Modelo 5

Demanda uniforme, con tasa de demanda d.
Escasez permitida, con coste p.
Coste de pedido: k.
Coste material constante.
Coste de almacenamiento h.
Conducción uniforme r>d. (En este caso, los pedidos no llegan instantáneamente)
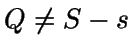Política (s,S): cuando se llega al nivel s se hace un pedido para llegar al nivel S. El pedido sigue llegando hasta que el nivel de inventario sea S. Luego en este caso $Q \neq S-s$ .

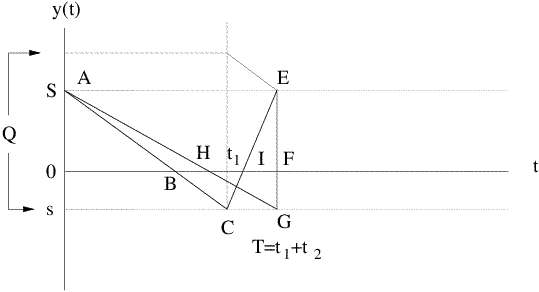
Vamos a relacionar este modelo con el modelo 1, pero considerando el período que define el segmento AG.

Para ello vamos a ver que en ambos modelos coinciden las respectivas áreas de los triángulos asociados con costes de almacenamiento por un lado y con costes de escasez por el otro.

$\begin{displaymath}\begin{array}{lcc} & \text{Modelo 5} & \text{Modelo 1} \\ \... ...to} & \widehat{AOB}+\widehat{IEF} & \widehat{AOH} \end{array}\end{displaymath}$

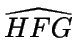Como $\widehat{IEF}$ y $\widehat{ABH}$ tienen la misma altura, si se prueba que tienen la misma base entonces tendrán la misma área. Se busca ver que BH=IF. Además, si se prueba esto entonces también $\widehat{BCI}$ y $\widehat{HFG}$ tendrán la misma base (y como tienen la misma altura, entonces tendrán áreas iguales):

BI = BH + HI = IF + HI = HF.

Así pues, veamos que BH=IF. La recta que pasa por A y C es y(t)=S-dt, por lo que

$\begin{displaymath}B = \left( \frac{S}{d},0 \right), \quad C=\left( \frac{S-s}{d},s \right).\end{displaymath}$

Además,

$\begin{displaymath}E= \left( \frac{S-s}{d} + \frac{S-s}{r-d},S \right)= \left( (S-s)\frac{r}{d(r-d)}, S \right).\end{displaymath}$

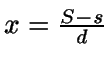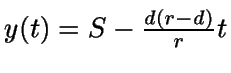(La coordenada en x se calcula observando que desde $x=\frac{S-s}{d}$ se sube S-s unidades uniformemente a ritmo r-s) De este modo, la recta que pasa por A y G es $y(t)=S-\frac{d(r-d)}{r}t$ . Luego

$\begin{displaymath}H=\left( \frac{Sr} {d(r-d)}, 0 \right).\end{displaymath}$

Por otra parte, la recta que pasa por C y E es

$\begin{displaymath}y(t)=S-\frac{r(S-s)}{d} + (r-d)t,\end{displaymath}$

por lo que

$\begin{displaymath}I=\left( \frac{r(S-s)} {d(r-d)} - \frac{S}{r-d},0 \right).\end{displaymath}$

Ahora

$\begin{displaymath}IF= \frac{(S-s)r}{d(r-d)} - \frac {r(S-s)} {d(r-d)} + \frac {S} {r-d} = \frac {S} {r-d},\end{displaymath}$

$\begin{displaymath}BH = \frac {Sr} {d(r-d)} - \frac {S} {d} = \frac {S} {d} \le... ... \right) = \frac {S} {d} \frac {r-r+d}{r-d} = \frac {S} {r-d}.\end{displaymath}$

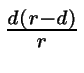En consecuencia, IF=BH. Ahora usamos los resultados del modelo 1 pero con tasa de demanda $\frac{d(r-d)}{r}$ :

$\begin{displaymath}S^*= \sqrt{\frac{2kd(r-d)}{hr}} \sqrt{\frac{p}{p+h}},\end{displaymath}$

$\begin{displaymath}s^*=-\sqrt{\frac{2kd(r-d)}{hr}} \sqrt{\frac{h}{p+h}}.\end{displaymath}$