
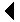

Siguiente: Aplicaciones de la simulación
Nivel anterior: Métodos específicos de generación de vv.aa.
Previa: Generación de variables continuas
- Si las componentes son independientes, se generan por separado.
- Si X es discreta, se trabaja como si fuese una variable
unidimensional.
Sea X continua con densidad
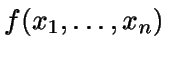 .
Siempre se puede
usar aceptación y rechazo, composición, etc., pues son métodos
generales. También se puede considerar la descomposición de f
como producto de densidades condicionadas e ir generando
progresivamente valores asociados a estas nuevas variables
unidimensionales.
.
Siempre se puede
usar aceptación y rechazo, composición, etc., pues son métodos
generales. También se puede considerar la descomposición de f
como producto de densidades condicionadas e ir generando
progresivamente valores asociados a estas nuevas variables
unidimensionales.
Se genera
Ejemplo:
Si comenzamos condicionando por x1:
No podemos despejar x1. Sin embargo, si empezamos
condicionando por la otra variable:
Cada par (x1,x2) se obtiene como
La última igualdad se debe a que si U es U(0,1),
entonces 1-U también sigue una distribución U(0,1).
Distribución normal multivariante
Para simular una variable
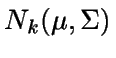 basta considerar las
dos siguientes observaciones:
basta considerar las
dos siguientes observaciones:
- Si se quiere simular una variable
Nk(0,Ik), basta simular k
valores N(0,1) (por la independencia de las componentes).
- Si
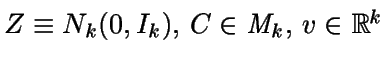 ,
entonces
,
entonces
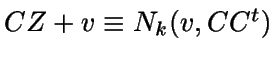 .
.
En consecuencia, tomando 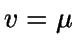 y C tal que
y C tal que
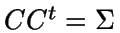 ,
se
obtiene un método para simular una variable normal
multivariante cualquiera. En particular, la matriz C se puede
tomar triangular inferior, en cuyo caso
,
se
obtiene un método para simular una variable normal
multivariante cualquiera. En particular, la matriz C se puede
tomar triangular inferior, en cuyo caso

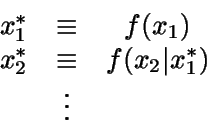
![]() basta considerar las
dos siguientes observaciones:
basta considerar las
dos siguientes observaciones: