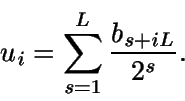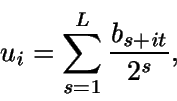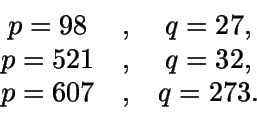


Siguiente: Métodos generales de generación de vv.aa.
Nivel anterior: Métodos de generación de vv.aa.
Previa: Métodos congruenciales
Sean 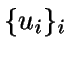 ,
,
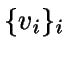 dos sucesiones de números pseudoaleatorios, generados congruencialmente, con respectivos
períodos c1 y c2. La sucesión
dos sucesiones de números pseudoaleatorios, generados congruencialmente, con respectivos
períodos c1 y c2. La sucesión
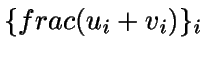 tiene
período
mcm(c1,c2).
Sean U1, U2 variables aleotorias independientes
con distribución U(0,1). La variable
Z=frac(U1+U2) sigue
también una distribución U(0,1).
tiene
período
mcm(c1,c2).
Sean U1, U2 variables aleotorias independientes
con distribución U(0,1). La variable
Z=frac(U1+U2) sigue
también una distribución U(0,1).
Demostración:
Como U1, U2 son independientes, entonces la variable
bidimensional (U1,U2) sigue una distribución uniforme en el
cuadrado
![$[0,1]\times [0,1]$](img354.gif) .
.
Sean
La distribución marginal es
Por otra parte,
Así, para
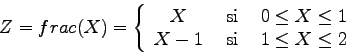 ,
se tiene
,
se tiene
Q.E.D.
Generadores binarios de cambio de registro
Representemos por bi el bit i-ésimo.
Partiendo de una semilla
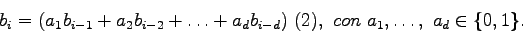 ,
se obtiene el bit i-ésimo a partir de una
combinación lineal de los anteriores:
,
se obtiene el bit i-ésimo a partir de una
combinación lineal de los anteriores:
Los ciclos serán de longitud 2d-1 a lo sumo (suponiendo
ad=1). Si se obtiene d veces consecutivas el valor 0,
entonces el algoritmo degenera generando siempre este valor.
Usualmente se procede como sigue: se toma p>q y se hace
El ciclo así generado tendrá una longitud de a lo sumo 2p-1 bits.
Si se quiere generar números pseudoaleatorios con precisión 2-L, se toma
Con el fin de ahorrar esfuerzo de cálculo se suele tomar (método sugerido por
Taustworthe)
donde t se denomina decimación. Así se tiene que el período máximo se
alcanza cuando se cumple
mcd(t,2p-1)=1. Los valores más
habituales son

![]() ,
se obtiene el bit i-ésimo a partir de una
combinación lineal de los anteriores:
,
se obtiene el bit i-ésimo a partir de una
combinación lineal de los anteriores: