

Siguiente: Otros métodos de generación de vv.aa.
Nivel anterior: Métodos de generación de vv.aa.
Previa: Introducción
Se define el siguiente método congruencial:
Se genera
a partir de una semilla X0, con
Entonces se toma
Ejemplo:
M=1000, a=7, c=501, X0=0.
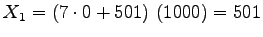 .
.
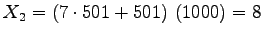 .
.
Y así sucesivamente.
Si
Xi=Xi+k por vez primera, entonces k se denomina
período del generador. Si c=0 el método se dice multiplicativo.
A continuación, enunciamos dos resultados relacionados con
congruencias cuya demostración se omite.
Condición necesaria para que un generador
multiplicativo tenga un período de longitud M-1 es que
M sea primo. Si M es primo, el período divide a M-1. En
este caso, el período es M-1 si, y sólo si,
Sea 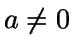 .
Un generador congruencial tiene
período M si, y sólo si, se cumplen las tres condiciones
siguientes:
.
Un generador congruencial tiene
período M si, y sólo si, se cumplen las tres condiciones
siguientes:
- 1.
-
mcd(c,M)=1.
- 2.
-
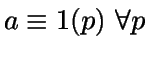 factor primo de M.
factor primo de M.
- 3.
-
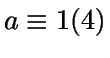 si M es múltiplo de 4.
si M es múltiplo de 4.
A continuación se presenta el generador implementado en los IBM380
en 1970. Este método resultó tener un gran problema: hay quince
planos paralelos en el cubo [0,1]3 que contienen todos los
puntos que se obtienen tomando tres valores Xi, Xi+1, Xi+2 cualesquiera.
Ejemplo: c=0,
a=216+3, M=231
Los ci que se utilizan a continuación representan enteros. Su
valor exacto se omite pues no tiene interés.
Xi+1=(216+3) Xi + 231 c0
=(6 (216+3)-9) Xi + 231 c4 = 6 (216+3)Xi - 9 Xi + 231
c4 = 6 Xi+1 -9 Xi + 231 c5
Así
Como ui, ui+1,
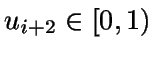 y
y
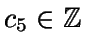 ,
enonces
,
enonces
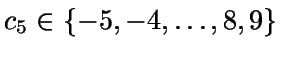 .
Es decir, todas las ternas
(ui,ui+1,ui+2) están concentradas en quince planos.
.
Es decir, todas las ternas
(ui,ui+1,ui+2) están concentradas en quince planos.
Un generador recomendado es
